Vòng tròn có bao nhiêu trục đối xứng?
các trục đối xứng của một vòng tròn Chúng là vô hạn. Các trục này là những trục chia bất kỳ hình dạng hình học thành hai nửa chính xác bằng nhau.
Và một vòng tròn bao gồm tất cả các điểm có khoảng cách đến một điểm cố định nhỏ hơn hoặc bằng một giá trị nhất định "r".
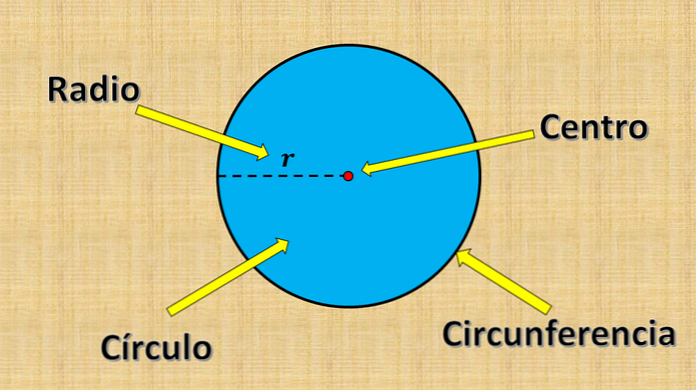
Điểm cố định được đề cập ở trên được gọi là tâm và giá trị "r" được gọi là bán kính. Bán kính là khoảng cách lớn nhất có thể có giữa một điểm trên đường tròn và tâm.
Mặt khác, bất kỳ đoạn đường nào có đầu nằm ở rìa của vòng tròn (chu vi) và đi qua tâm được gọi là đường kính. Số đo của nó luôn bằng hai lần bán kính.
Vòng tròn và chu vi
Đừng nhầm lẫn một vòng tròn với một vòng tròn. Chu vi chỉ đề cập đến các điểm ở khoảng cách "r" từ tâm; đó là, chỉ có cạnh của vòng tròn.
Tuy nhiên, khi tìm kiếm các trục đối xứng, nó không quan tâm nếu bạn làm việc với một vòng tròn hoặc với một vòng tròn.
Trục đối xứng là gì?
Một trục đối xứng là một đường chia thành hai phần bằng nhau một hình hình học nhất định. Nói cách khác, một trục đối xứng hoạt động như một tấm gương.
Trục đối xứng của một vòng tròn
Nếu bạn quan sát bất kỳ vòng tròn nào, bất kể bán kính của nó, bạn có thể thấy rằng không phải mọi đường thẳng đi qua nó đều là một trục đối xứng.
Ví dụ, không có đường nào được vẽ trong hình sau đây là trục đối xứng.
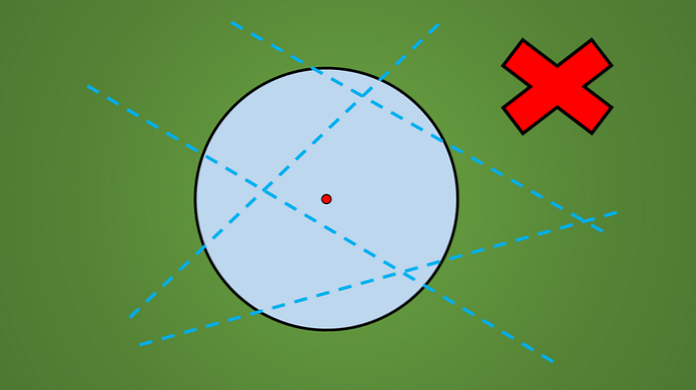
Một cách dễ dàng để kiểm tra xem một đường thẳng có phải là trục đối xứng hay không, là phản xạ vuông góc với hình hình học với phía đối diện của đường thẳng.
Nếu sự phản chiếu không phù hợp với hình gốc, thì đường thẳng đó không phải là trục đối xứng. Hình ảnh sau đây minh họa kỹ thuật này.
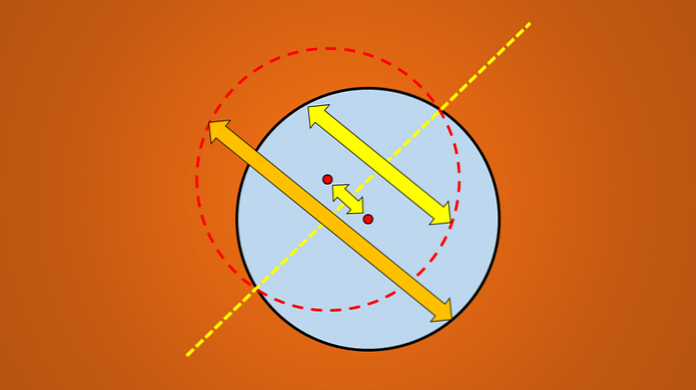
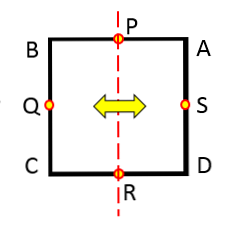
Nhưng nếu xem xét hình ảnh sau đây, thì ai cũng biết rằng đường được vẽ là một trục đối xứng của đường tròn.
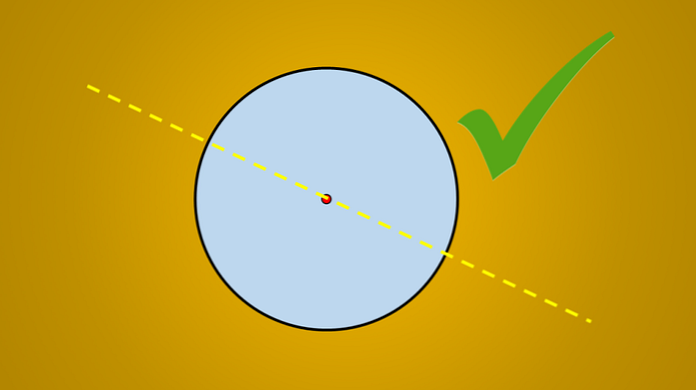
Câu hỏi là: có nhiều trục đối xứng không? Câu trả lời là có. Nếu bạn xoay dòng này 45 ° ngược chiều kim đồng hồ, dòng thu được cũng là một trục đối xứng của vòng tròn.
Điều tương tự cũng xảy ra nếu bạn xoay 90 °, 30 °, 8 ° và nói chung, bất kỳ số độ nào.
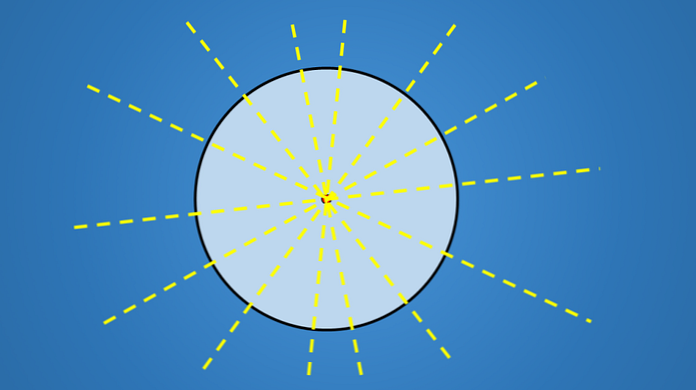
Điều quan trọng về những đường này không phải là độ nghiêng mà chúng có, mà tất cả chúng đều đi qua tâm của vòng tròn. Do đó, bất kỳ đường thẳng nào chứa đường kính của vòng tròn là một trục đối xứng.
Vì vậy, vì một đường tròn có số lượng đường kính vô hạn, nên nó có vô số trục đối xứng.
Các hình hình học khác, chẳng hạn như hình tam giác, hình tứ giác, hình ngũ giác, hình lục giác hoặc bất kỳ hình đa giác nào khác, có số lượng trục đối xứng hữu hạn.
Lý do tại sao một vòng tròn có vô số trục đối xứng là vì nó không có cạnh.
Tài liệu tham khảo
- Basto, J. R. (2014). Toán 3: Hình học phân tích cơ bản. Nhóm biên tập Patria.
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Toán học: cách tiếp cận giải quyết vấn đề cho giáo viên giáo dục cơ bản. Biên tập viên López Mateos.
- Bult, B., & Hobbs, D. (2001). Toán từ vựng (minh họa ed.). (F. P. Cadena, Trad.) Ấn bản AKAL.
- Callejo, I., Aguilera, M., Martinez, L., & Aldea, C. (1986). Toán học Hình học Cải cách chu kỳ trên của E.G.B. Bộ giáo dục.
- Schneider, W., & Sappert, D. (1990). Hướng dẫn vẽ kỹ thuật thực hành: giới thiệu những điều cơ bản của bản vẽ kỹ thuật công nghiệp. Reverte.
- Thomas, G. B., & Weir, M. D. (2006). Tính toán: một số biến. Giáo dục Pearson.


