Hệ thống và ví dụ Colinear
các vectơ colinear Chúng là một trong ba loại vectơ hiện có. Đó là về những vectơ có cùng hướng hoặc đường hành động. Điều này có nghĩa như sau: hai hoặc nhiều vectơ sẽ được cộng tuyến nếu chúng được sắp xếp theo các đường thẳng song song với nhau.
Một vectơ được định nghĩa là một đại lượng được áp dụng cho một cơ thể và được đặc trưng là có hướng, ý nghĩa và tỷ lệ. Các vectơ có thể được tìm thấy trong mặt phẳng hoặc trong không gian và có thể có các loại khác nhau: vectơ colinear, vectơ đồng thời và vectơ song song.

Chỉ số
- 1 vectơ đại tràng
- 2 Đặc điểm
- 2.1 Ví dụ 1
- 2.2 Ví dụ 2
- 2.3 Ví dụ 1
- Hệ thống vectơ 3
- 3.1 Các vectơ cộng tuyến với các giác quan ngược nhau
- 3.2 Các vectơ cộng tuyến có cùng ý nghĩa
- 3.3 Các vectơ cộng tuyến có cường độ bằng nhau và các giác quan ngược nhau
- 4 Sự khác biệt giữa vectơ colinear và đồng thời
- 5 tài liệu tham khảo
Vectơ cộng tuyến
Các vectơ là cộng tuyến nếu dòng hành động của một chính xác là cùng một dòng hành động của tất cả các vectơ khác, bất kể kích thước và ý nghĩa của từng vectơ.
Các vectơ được sử dụng làm biểu diễn trong các lĩnh vực khác nhau như toán học, vật lý, đại số và cả trong hình học, trong đó các vectơ chỉ được cộng tuyến khi hướng của chúng giống nhau, bất kể ý nghĩa của chúng không phải là.
Tính năng
- Hai hoặc nhiều vectơ là cộng tuyến nếu mối quan hệ giữa các tọa độ bằng nhau.
Ví dụ 1
Chúng ta có các vectơ m = m_x; m_y và n = n_x; n_y. Đây là các collinear nếu:
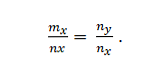
Ví dụ 2
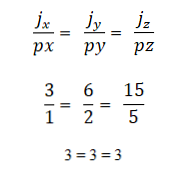
- Hai hoặc nhiều vectơ là cộng tuyến nếu phép nhân của sản phẩm hoặc vectơ bằng 0 (0). Điều này là do, trong hệ tọa độ, mỗi vectơ được đặc trưng bởi tọa độ tương ứng của nó và nếu các tỷ lệ này tỷ lệ với nhau, các vectơ sẽ được cộng tuyến. Điều này được thể hiện như sau:
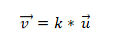
Ví dụ 1
Ta có các vectơ a = (10, 5) và b = (6, 3). Để xác định xem chúng có được cộng tuyến hay không, lý thuyết xác định được áp dụng, điều này thiết lập sự bình đẳng của các sản phẩm chéo. Theo cách đó, bạn phải:
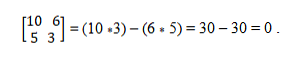
Hệ thống vectơ colinear
Các vectơ colinear được biểu thị bằng đồ họa bằng cách sử dụng hướng và ý nghĩa của những điều này - cho rằng chúng phải đi qua điểm ứng dụng - và mô-đun, có tỷ lệ hoặc độ dài nhất định.
Hệ thống các vectơ cộng tuyến được hình thành khi hai hoặc nhiều vectơ tác dụng lên một vật hoặc cơ thể, đại diện cho một lực và tác dụng theo cùng một hướng.
Ví dụ, nếu hai lực cộng tuyến được áp dụng trên một cơ thể, kết quả của những lực này sẽ chỉ phụ thuộc vào hướng mà chúng hành động. Có ba trường hợp, đó là:
Các vectơ cộng tuyến với các giác quan ngược nhau
Kết quả của hai vectơ cộng tuyến bằng tổng của các vectơ này:
R = Σ F = F1 + F2.
Ví dụ
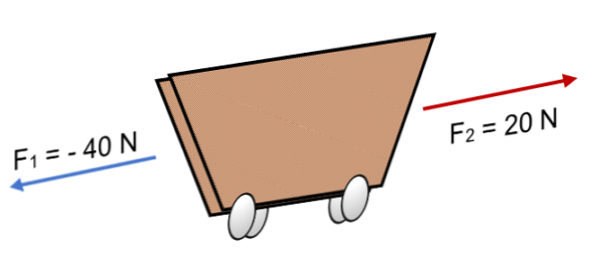
Nếu hai lực tác dụng lên xe đẩy F1 = 40 N và F2 = 20 N theo hướng ngược lại (như trong hình), kết quả là:
R = Σ F = (- 40 N) + 20N.
R = - 20 N.
Các vectơ cộng tuyến có cùng ý nghĩa
Độ lớn của lực tổng hợp sẽ bằng tổng các vectơ cộng tuyến:
R = Σ F = F1 + F2.
Ví dụ
Nếu hai lực tác dụng lên xe đẩy F1 = 35 N và F2 = 55 N theo cùng một hướng (như trong hình), kết quả là:
R = Σ F = 35 N + 55N.
R = 90 N.
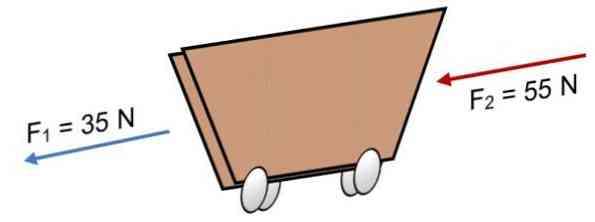
Kết quả dương cho thấy các vectơ cộng tuyến tác động về phía bên trái.
Các vectơ cộng tuyến có độ lớn bằng nhau và các giác quan ngược nhau
Kết quả của hai vectơ cộng tuyến sẽ bằng tổng các vectơ cộng tuyến:
R = Σ F = F1 + F2.
Vì các lực có cùng độ lớn nhưng theo hướng ngược lại - đó là, một sẽ có giá trị dương và một lực khác-, khi thêm hai lực, kết quả sẽ bằng không.
Ví dụ
Nếu hai lực tác dụng lên xe đẩy F1 = -7 N và F2 = 7 N, có cùng độ lớn nhưng theo hướng ngược lại (như trong hình), kết quả là:
R = Σ F = (-7 N) + 7N.
R = 0.
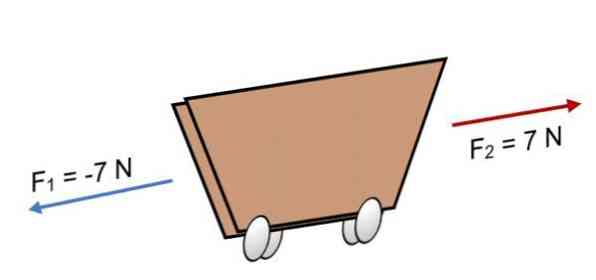
Vì kết quả bằng 0, có nghĩa là các vectơ được cân bằng với nhau và do đó, cơ thể ở trạng thái cân bằng hoặc ở trạng thái nghỉ (nó sẽ không di chuyển).
Sự khác biệt giữa vectơ colinear và đồng thời
Các vectơ collinear được đặc trưng bởi có cùng hướng trên cùng một đường hoặc bởi vì chúng song song với một đường; đó là, chúng là các vectơ đường thẳng song song.
Mặt khác, các vectơ đồng thời được xác định bởi vì chúng nằm trong các dòng hành động khác nhau bị chặn trong một điểm duy nhất.
Nói cách khác, chúng có cùng điểm xuất phát hoặc điểm đến - bất kể mô-đun, hướng hay hướng của chúng -, tạo thành một góc giữa chúng.
Các hệ thống vectơ đồng thời được giải bằng các phương pháp toán học hoặc đồ thị, là phương pháp của hình bình hành của các lực và phương pháp của đa giác của các lực. Thông qua các giá trị của một vectơ kết quả sẽ được xác định, cho biết hướng mà cơ thể sẽ di chuyển.
Về cơ bản, sự khác biệt chính giữa các vectơ colinear và vectơ đồng thời là dòng hành động trong đó chúng hoạt động: các collinear hoạt động trong cùng một dòng, trong khi các vectơ đồng thời khác nhau.
Đó là, các vectơ cộng tuyến hoạt động trong một mặt phẳng, "X" hoặc "Y"; và hành động đồng thời ở cả hai mặt phẳng, bắt đầu từ cùng một điểm.
Các vectơ cộng tuyến không nằm trong một điểm, cũng như các vectơ đồng thời, vì chúng song song với nhau.
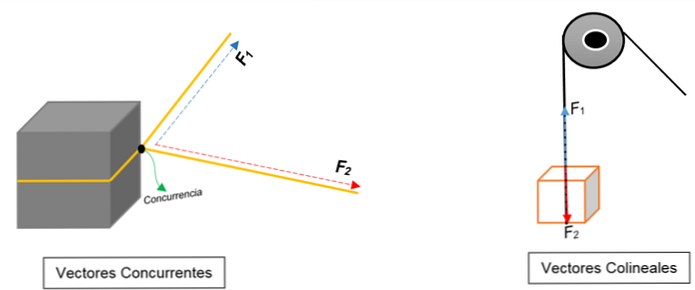
Trong hình ảnh bên trái, bạn có thể thấy một khối. Nó được buộc bằng một sợi dây và nút thắt chia làm hai; khi được kéo về các hướng khác nhau và với các lực khác nhau, khối sẽ di chuyển về cùng một hướng.
Hai vectơ được biểu diễn đồng quy trong một điểm (khối), bất kể mô-đun, ý nghĩa hoặc hướng của chúng.
Thay vào đó, trong hình ảnh bên phải xuất hiện một ròng rọc nâng một hộp. Sợi dây đại diện cho dòng hành động; khi nó được kéo, hai lực (vectơ) tác dụng lên nó: một lực căng (khi leo lên khối) và một lực khác, lực tác dụng làm trọng lượng của khối. Cả hai đều có cùng một hướng nhưng theo hướng ngược lại; không đồng tình ở một điểm.
Tài liệu tham khảo
- Estalella, J. J. (1988). Phân tích véc tơ. Tập 1.
- Gupta, A. (s.f.). Giáo dục Tata McGraw-Hill.
- Jin Ho Kwak, S. H. (2015). Đại số tuyến tính. Khoa học & Truyền thông kinh doanh Springer.
- Montiel, H. P. (2000). Vật lý 1 cho tú tài công nghệ. Nhóm biên tập Patria.
- Santiago Burbano de Ercilla, C. G. (2003). Vật lý đại cương Thanh công cụ biên tập.
- Sinha, K. (s.f.). Sách giáo khoa Toán học XII Tập 2. Ấn phẩm Rastogi.


