Tiểu sử, đóng góp và phát minh của Archimedes
Archimedes của Syracuse (287 a.C - 212 a.C) là một nhà toán học, nhà vật lý, nhà phát minh, kỹ sư và nhà thiên văn học Hy Lạp đến từ thành phố cổ Syracuse, trên đảo Sicily. Những đóng góp nổi bật nhất của ông là nguyên tắc Archimedes, sự phát triển của phương pháp xả khí, phương pháp cơ học hoặc tạo ra cung thiên văn đầu tiên.
Tại thời điểm này, nó được coi là một trong ba nhân vật quan trọng hơn của toán học Cổ vật bên cạnh Euclide và Apolonio, vì những đóng góp của nó có nghĩa là những tiến bộ khoa học quan trọng cho thời gian trong các lĩnh vực tính toán, vật lý, hình học và thiên văn học. Đổi lại, điều này làm cho anh ta trở thành một trong những nhà khoa học xuất sắc nhất trong lịch sử nhân loại.

Mặc dù có rất ít chi tiết về cuộc sống cá nhân của anh ta - và những người được biết là có độ tin cậy đáng ngờ - nhưng những đóng góp của anh ta được biết đến nhờ một loạt các lá thư viết về các tác phẩm và thành tựu của anh ta được bảo tồn cho đến hiện tại, thuộc về với sự tương ứng mà ông đã giữ trong nhiều năm với bạn bè và các nhà toán học khác cùng thời.
Archimedes nổi tiếng trong thời đại của ông nhờ những phát minh của ông, đã thu hút sự chú ý của những người cùng thời, một phần vì chúng được sử dụng như thiết bị chiến tranh để tránh thành công nhiều cuộc xâm lược của La Mã..
Tuy nhiên, người ta nói rằng ông tuyên bố rằng điều thực sự quan trọng duy nhất là toán học, và những phát minh của ông chỉ là một sản phẩm của trò tiêu khiển của hình học ứng dụng. Trong hậu thế, các tác phẩm của ông trong toán học thuần túy đã được đánh giá cao hơn nhiều so với các phát minh của ông.
Chỉ số
- 1 Tiểu sử
- 1.1 Đào tạo
- 1.2 Công trình khoa học
- 1.3 Xung đột ở Syracuse
- 1.4 Cái chết
- 2 Đóng góp khoa học của Archimedes
- 2.1 Nguyên tắc của Archimedes
- 2.2 Phương pháp cơ học
- 2.3 Giải thích về luật đòn bẩy
- 2.4 Phát triển phương pháp cạn kiệt hoặc cạn kiệt cho trình diễn khoa học
- 2.5 Số đo của vòng tròn
- 2.6 Hình dạng của hình cầu và hình trụ
- 3 phát minh
- 3.1 Máy đo đường
- 3.2 Cung thiên văn đầu tiên
- 3.3 Vít Archimedes
- 3.4 Móng vuốt của Archimedes
- 4 tài liệu tham khảo
Tiểu sử
Archimedes of Syracuse ra đời vào khoảng năm 287 trước Công nguyên. Không có nhiều thông tin được biết về những năm đầu của anh ấy, mặc dù có thể nói rằng anh ấy được sinh ra ở Syracuse, một thành phố được coi là cảng biển chính của đảo Sicily, ngày nay ở Ý..
Vào thời điểm đó, Syracuse là một trong những thành phố tạo nên cái gọi là Magna Grecia, là không gian của những người định cư gốc Hy Lạp đến khu vực phía nam của bán đảo Ý và Sicily.
Không có sự thật được biết đến về mẹ của Archimedes. Liên quan đến người cha, người ta biết rằng đây được gọi là Phidias và ông được dành riêng cho thiên văn học. Thông tin này của cha anh được biết đến nhờ một mảnh của cuốn sách Quầy cát, được viết bởi Archimedes, trong đó ông đề cập đến tên của cha mình.
Heraklides, một nhà triết học và thiên văn học người Hy Lạp, rất thích Archimedes và thậm chí đã viết tiểu sử về ông. Tuy nhiên, tài liệu đó chưa được lưu giữ, vì vậy tất cả thông tin có trong đó là không xác định.
Mặt khác, nhà sử học, triết gia và nhà viết tiểu sử Plutarco đã chỉ ra trong cuốn sách của mình có tựa đề Parallel Lives mà Archimedes có mối quan hệ huyết thống với Hiero II, một bạo chúa đã từng nắm quyền ở Syracuse từ năm 265 trước Công nguyên.
Đào tạo
Do kết quả của những thông tin nhỏ mà chúng tôi có về Archimedes, chúng tôi không biết chắc chắn nơi anh ấy đã được đào tạo đầu tiên.
Tuy nhiên, nhiều nhà sử học khác nhau đã xác định rằng có khả năng cao Arch Arches đã nghiên cứu ở Alexandria, đây là trung tâm giảng dạy và văn hóa quan trọng nhất của Hy Lạp trong khu vực..
Giả định này được hỗ trợ bởi thông tin được cung cấp bởi nhà sử học Hy Lạp Diodoro Sículo, người chỉ ra rằng Archimedes có lẽ đã nghiên cứu ở Alexandria.
Ngoài ra, trong nhiều tác phẩm của mình, Archimedes đã đề cập đến các nhà khoa học khác thời đó có công việc tập trung ở Alexandria, vì vậy có thể giả định rằng ông thực sự phát triển ở thành phố đó.
Một số tính cách mà Archimedes được cho là đã tương tác ở Alexandria là nhà địa lý học, nhà toán học và nhà thiên văn học Eratosthenes của Cyrene, và nhà toán học và nhà thiên văn học Conon de Sanos.
Động lực gia đình
Mặt khác, việc cha của Archimedes là một nhà thiên văn học có thể có ảnh hưởng đáng kể đến các khuynh hướng mà sau đó ông đã thể hiện, bởi vì sau này và từ khi còn trẻ, có một sức hấp dẫn đặc biệt trong lĩnh vực khoa học.
Sau thời gian ở Alexandria, người ta ước tính Archimedes trở lại Syracuse.
Công việc khoa học
Sau khi trở về Syracuse, Archimedes bắt đầu nghĩ ra những cổ vật khác nhau đã sớm mang lại cho anh một sự nổi tiếng nhất định trong cư dân của thành phố này. Trong thời kỳ này, ông đã cống hiến hoàn toàn cho công việc khoa học, tạo ra những phát minh khác nhau và suy luận một số khái niệm toán học rất tiến bộ vào thời đại của ông.
Ví dụ, khi ông dành hết tâm huyết cho việc nghiên cứu các đặc điểm của các hình cong và phẳng đặc, ông đã đưa ra các khái niệm liên quan đến phép tính tích phân và vi phân, được phát triển sau này.
Ngoài ra, Archimedes là người đã xác định rằng thể tích liên kết với một hình cầu tương ứng với hai lần kích thước của hình trụ chứa nó, và là người đã phát minh ra ròng rọc hỗn hợp, dựa trên những khám phá của ông về định luật của đòn bẩy.
Xung đột ở Syracuse
Trong năm 213 trước Công nguyên, những người lính La Mã đã vào thành phố Syracuse và bao vây những người định cư của nó để khiến họ đầu hàng.
Hành động này được lãnh đạo bởi chính trị gia quân sự và Hy Lạp Marco Claudio Marcelo trong khuôn khổ Chiến tranh Punic lần thứ hai. Sau đó, nó được gọi là Thanh kiếm của Rome, vì cuối cùng nó đã chinh phục được Syracuse.
Ở giữa cuộc xung đột kéo dài hai năm, cư dân ở vùng Syracuse đã chiến đấu chống lại người La Mã với lòng can đảm và quyết liệt, và Archimedes đã đóng một vai trò rất quan trọng, vì ông đã tận tâm tạo ra các công cụ và dụng cụ giúp đánh bại người La Mã.
Cuối cùng, Marco Claudio Marcelo đã chiếm thành phố Syracuse. Trước trí tuệ tuyệt vời của Archimedes, Marcelo đã ra lệnh rằng họ không bị tổn thương hay bị giết. Tuy nhiên, Archimedes đã bị giết trong tay của một người lính La Mã.
Cái chết
Archimedes đã chết vào năm 212 trước Công nguyên. Hơn 130 năm sau khi ông qua đời, vào năm 137 trước Công nguyên, nhà văn, chính trị gia và triết gia Marco Tulio Cicero đã chiếm một vị trí trong chính quyền của Rome và muốn tìm mộ của Archimedes.
Nhiệm vụ này không dễ dàng, vì Cicero không thể tìm thấy ai để chỉ ra địa điểm chính xác. Tuy nhiên, cuối cùng anh đã có được nó, rất gần với cánh cửa của Agrigento và trong điều kiện tồi tệ.
Cicero đã làm sạch ngôi mộ và phát hiện ra rằng nó được khắc một quả cầu bên trong một hình trụ, như một tài liệu tham khảo về khám phá về khối lượng mà Archimedes đã thực hiện một thời gian trước đây..
Phiên bản về cái chết của anh ấy
Phiên bản đầu tiên
Một trong những phiên bản nói rằng Archimedes đang ở giữa giải quyết một vấn đề toán học khi anh ta được một người lính La Mã tiếp cận. Người ta nói rằng Archimedes có thể đã yêu cầu anh ta một thời gian để giải quyết vấn đề, vì vậy người lính sẽ giết anh ta.
Phiên bản thứ hai
Phiên bản thứ hai tương tự như phiên bản đầu tiên. Tài khoản mà Archimedes đang giải quyết một vấn đề toán học khi việc chiếm thành phố xảy ra.
Một người lính La Mã đã vào khu tập thể của anh ta và ra lệnh cho anh ta gặp Marcelo, và Archimedes trả lời rằng anh ta phải giải quyết vấn đề mà anh ta đang làm việc trước tiên. Người lính buồn bã vì phản ứng này và giết chết anh ta.
Phiên bản thứ ba
Giả thuyết này chỉ ra rằng Archimedes đã có trong tay một sự đa dạng lớn về các công cụ điển hình của toán học. Sau đó, một người lính nhìn thấy anh ta và anh ta nghĩ rằng anh ta có thể mang theo những vật phẩm có giá trị, vì vậy anh ta đã giết anh ta.
Phiên bản thứ tư
Phiên bản này minh họa rằng Archimedes đã cúi xuống gần mặt đất, dự tính những kế hoạch mà ông đang nghiên cứu. Rõ ràng, một người lính La Mã đến từ phía sau và, không biết rằng đó là Archimedes, đã bắn anh ta.
Đóng góp khoa học của Archimedes
Nguyên tắc của Archimedes
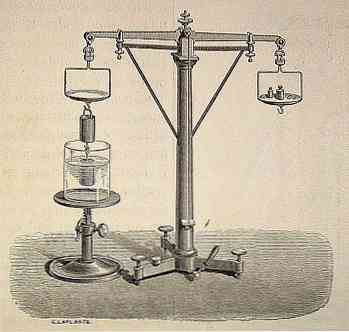
Nguyên lý của Archimedes được khoa học hiện đại coi là một trong những di sản quan trọng nhất của thời kỳ cổ đại.
Trong suốt lịch sử và bằng miệng, có thông tin rằng Archimedes đã vô tình đến khám phá của ông nhờ vua Hieron ủy thác để xem nếu một vương miện vàng, được gửi đến sản xuất bởi ông, chỉ được làm bằng vàng nguyên chất và không chứa bất kỳ kim loại nào khác. Tôi đã phải thực hiện điều này mà không phá hủy vương miện.
Người ta nói rằng trong khi Archimedes đang thiền định cách giải quyết vấn đề này, anh ta quyết định đi tắm, và khi anh ta bước vào bồn tắm, anh ta nhận ra rằng nước tăng lên khi anh ta đắm mình trong đó..
Bằng cách này, anh ta sẽ khám phá ra nguyên tắc khoa học rằng "mọi cơ thể chìm hoàn toàn hoặc một phần trong chất lỏng (chất lỏng hoặc khí) đều nhận được lực đẩy lên, bằng trọng lượng của chất lỏng bị vật thể đánh bật".
Nguyên tắc này có nghĩa là các chất lỏng tác dụng một lực tăng dần - đẩy lên trên - trên bất kỳ vật nào được ngâm trong chúng, và lượng lực đẩy này bằng với trọng lượng của chất lỏng được di chuyển bởi cơ thể chìm, bất kể trọng lượng của nó.
Giải thích về nguyên tắc này mô tả hiện tượng tuyển nổi, và được tìm thấy trong nó Hiệp ước về các cơ quan nổi.
Nguyên tắc của Archimedes đã được áp dụng rất nhiều trong hậu thế cho việc thả nổi các vật thể được sử dụng lớn như tàu ngầm, tàu, nhân viên cứu hộ và bóng bay.
Phương pháp cơ khí
Một trong những đóng góp quan trọng nhất của Archimedes đối với khoa học là sự bao gồm một phương pháp hoàn toàn cơ học - đó là phương pháp kỹ thuật trong lý luận và lập luận về các vấn đề hình học, có nghĩa là một cách chưa từng có để giải quyết loại vấn đề này vào thời điểm đó.
Trong bối cảnh của Archimedes, hình học được coi là một môn khoa học lý thuyết độc quyền, và điều phổ biến là toán học thuần túy được truyền vào các ngành khoa học thực tế khác trong đó các nguyên tắc của nó có thể được áp dụng..
Vì lý do này, ngày nay nó được coi là tiền thân của cơ học như là một môn khoa học.
Trong bài viết mà nhà toán học đưa ra phương pháp mới cho người bạn Eratosthenes của mình, chỉ ra rằng điều này cho phép giải quyết các vấn đề của toán học thông qua cơ học, và việc xây dựng một định lý hình học sẽ dễ dàng hơn có một số kiến thức thực tế trước đó, rằng nếu bạn không có ý tưởng gì về nó.
Phương pháp điều tra mới này do Archimedes thực hiện sẽ trở thành tiền thân của giai đoạn khám phá và xây dựng giả thuyết không chính thức của phương pháp khoa học hiện đại.
Giải thích về luật đòn bẩy
Mặc dù đòn bẩy là một cỗ máy đơn giản được sử dụng từ rất sớm so với Archimedes, nhưng chính ông là người đã xây dựng nguyên tắc giải thích hoạt động của nó trong chuyên luận về sự cân bằng của các mặt phẳng.
Trong công thức của luật này, Archimedes thiết lập các nguyên tắc mô tả hành vi khác nhau của đòn bẩy khi đặt hai cơ thể lên nó, tùy thuộc vào trọng lượng của nó và khoảng cách từ điểm hỗ trợ.
Bằng cách này, ông chỉ ra rằng hai cơ thể có khả năng đo (tương xứng), nằm trên một đòn bẩy, được cân bằng khi chúng ở khoảng cách tỷ lệ nghịch với trọng lượng của chúng.
Theo cách tương tự, các cơ quan vô lượng (không thể đo lường được) làm như vậy, nhưng luật này đã bị Archimedes chỉ đối xử với các cơ quan thuộc loại thứ nhất.
Công thức của nó về nguyên lý của đòn bẩy là một ví dụ điển hình cho việc áp dụng phương pháp cơ học, vì theo nó giải thích trong một lá thư gửi cho Dổngo, điều này đã được phát hiện trong một khoảnh khắc đầu tiên thông qua các phương pháp của cơ học đưa vào thực tế.
Sau đó, ông đã xây dựng chúng bằng các phương pháp hình học (lý thuyết). Từ thí nghiệm này trên cơ thể, khái niệm trọng tâm đã bị tách ra.
Phát triển phương pháp kiệt sức hoặc cạn kiệt cho trình diễn khoa học
Kiệt sức là một phương pháp được sử dụng trong hình học bao gồm xấp xỉ các hình hình học có diện tích được biết đến, bằng phương pháp ghi và cắt, trên một hình khác có diện tích dự định được biết..
Mặc dù Archimedes không phải là người tạo ra phương pháp này, ông đã phát triển nó một cách thành thạo, quản lý để tính toán bằng phương pháp giá trị chính xác của Pi.
Archimedes, sử dụng phương pháp rút gọn, các hình lục giác được ghi và cắt theo chu vi đường kính 1, làm giảm sự khác biệt giữa diện tích của hình lục giác và chu vi.
Để làm điều này, anh ta chia đôi các hình lục giác tạo ra các đa giác có tới 16 cạnh, như trong hình trước.
Bằng cách này, anh ta đã xác định rằng giá trị của pi (của mối quan hệ giữa chiều dài của một vòng tròn và đường kính của nó) nằm giữa các giá trị 3.14084507 ... và 3.14285714 ... .
Archimedes đã sử dụng thành thạo phương pháp exhaución vì không chỉ quản lý để tính gần đúng giá trị của Pi với biên sai số khá thấp, và do đó, mong muốn, mà còn bởi vì Pi là một số vô tỷ phương pháp này và các kết quả thu được đã đặt nền móng sẽ nảy mầm trong hệ thống tính toán vô hạn, và sau đó, trong phép tính tích phân hiện đại.
Số đo của vòng tròn
Để xác định diện tích hình tròn, Archimedes đã sử dụng một phương pháp bao gồm vẽ một hình vuông khớp chính xác bên trong hình tròn.
Biết rằng diện tích của hình vuông là tổng của các cạnh của nó và diện tích của hình tròn lớn hơn, anh bắt đầu làm việc để đạt được xấp xỉ. Điều này ông đã làm bằng cách thay thế hình vuông bằng đa giác 6 cạnh và sau đó làm việc với các đa giác phức tạp hơn.
Archimedes là nhà toán học đầu tiên trong lịch sử tiếp cận việc tính toán nghiêm túc số Pi.
Hình dạng của hình cầu và hình trụ
Trong số chín chuyên luận biên soạn công trình của Archimedes trong toán học và vật lý, có hai tập về hình học của hình cầu và hình trụ.
Công việc này liên quan đến việc xác định rằng bề mặt của bất kỳ hình cầu bán kính nào gấp bốn lần hình tròn lớn nhất của nó và thể tích của một hình cầu bằng hai phần ba hình trụ mà nó được ghi.
Phát minh
Máy đo đường
Còn được gọi là km, đó là một phát minh của người đàn ông nổi tiếng này.
Thiết bị này được chế tạo dựa trên nguyên lý của một bánh xe, khi nó quay, kích hoạt các bánh răng cho phép tính quãng đường đi được..
Theo nguyên tắc tương tự, Archimedes đã thiết kế một số loại máy đo đường cho mục đích quân sự và dân sự.
Cung thiên văn đầu tiên
Dựa trên lời khai của nhiều nhà văn cổ điển như Cicero, Ovid, Claudian, Marciano Capela, Casiodoro, Sexto Empirico và Lactantius, nhiều nhà khoa học hiện đang gán cho Archimedes việc tạo ra cung thiên văn thô sơ đầu tiên.
Đó là một cơ chế được cấu thành bởi một loạt các "khối cầu" có khả năng bắt chước chuyển động của các hành tinh. Cho đến nay các chi tiết của cơ chế này vẫn chưa được biết.
Theo Cicero, các cung thiên văn được xây dựng bởi Archimedes là hai. Trong một trong số đó, vùng đất và các chòm sao khác nhau gần đó được đại diện.
Mặt khác, với một vòng quay duy nhất, mặt trời, mặt trăng và các hành tinh đã tạo ra các chuyển động độc lập của riêng chúng so với các ngôi sao cố định giống như cách chúng đã làm trong một ngày thực. Ngoài ra, sau đó, có thể được quan sát các giai đoạn và nhật thực liên tiếp của mặt trăng.
Các vít của Archimedes
Vít Archimedes là một thiết bị được sử dụng để vận chuyển nước từ dưới lên trên qua một con dốc, sử dụng ống hoặc xi lanh.
Theo nhà sử học Hy Lạp Diodoro, nhờ phát minh này, nó đã tạo điều kiện thuận lợi cho việc tưới tiêu của những vùng đất màu mỡ nằm dọc theo sông Nile ở Ai Cập cổ đại, vì các công cụ truyền thống đòi hỏi một nỗ lực thể chất to lớn làm cạn kiệt công nhân.
Xylanh được sử dụng có bên trong một ốc vít có cùng chiều dài, duy trì liên kết một hệ thống cánh quạt hoặc vây thực hiện chuyển động quay được điều khiển bằng tay bởi một đòn bẩy quay.
Theo cách này, các vòng xoắn quản lý để đẩy bất kỳ chất nào từ dưới lên, tạo thành một loại mạch vô hạn.
Móng vuốt của Archimedes
Móng vuốt của Archimedes, hay bàn tay sắt như nó cũng được biết đến, là một trong những vũ khí chiến tranh đáng sợ nhất được tạo ra bởi nhà toán học này, trở thành quan trọng nhất đối với sự bảo vệ của Sicily đối với các cuộc xâm lược của La Mã.
Theo nghiên cứu được thực hiện bởi các giáo sư của Đại học Drexel, Chris Rorres (Khoa Toán học) và Harry Harris (Khoa Kỹ thuật Xây dựng và Kiến trúc), đó là một đòn bẩy lớn có móc treo vào cần gạt bằng một chuỗi treo từ nó.
Thông qua đòn bẩy, lưỡi câu đã được điều khiển để nó rơi xuống tàu địch và mục tiêu là móc nó lên và nâng nó đến mức khi thả nó ra, nó có thể bị lật ngược hoàn toàn, hoặc đâm vào đá trên bờ..
Rorres và Harris đã trình bày tại Hội nghị chuyên đề "Máy móc và cấu trúc phi thường của thời cổ đại" (2001), một đại diện thu nhỏ của cổ vật này có tên "Một cỗ máy chiến tranh ghê gớm: Xây dựng và vận hành Bàn tay sắt của Archimedes"
Để hiện thực hóa tác phẩm này, họ đã dựa vào lập luận của các nhà sử học cổ đại Polibio, Plutarco và Tito Livio.
Tài liệu tham khảo
- ASSIS, A. (2008). Archimedes, trung tâm của trọng lực, và định luật cơ học đầu tiên [trực tuyến]. Truy cập ngày 10 tháng 6 năm 2017 trên bourabai.ru.
- DIJKSTERHUIS, E. (1956). Archimedes [trực tuyến]. Truy cập ngày 9 tháng 6 năm 2015 trên World Wide Web: Books.google.co.ve/books.
- MOLINA, A. (2008). Phương pháp nghiên cứu của Archimedes of Syracuse: trực giác, cơ học và sự cạn kiệt [trực tuyến]. Truy cập vào ngày 10 tháng 6 năm 2017 tại World Wide Webproduccionellectifica.luz.edu.
- O'CONNOR, J. & ROBERTSON, R. (1999). Archimedes của Syracuse [trực tuyến]. Truy cập ngày 9 tháng 6 năm 2017 tại history.mcs.st-and.ac.uk.
- PARRA, E. (2009). Archimedes: cuộc đời, công trình và những đóng góp của ông cho toán học hiện đại [trực tuyến]. Truy cập ngày 9 tháng 6 năm 2017 tại lfunes.uniandes.edu.co.
- QUINN, L. (2005). Archimedes của Syracuse [trực tuyến]. Truy cập ngày 9 tháng 6 năm 2017 tại math.ucdenver.edu.
- RORRES, C. & HARRIS, H. (2001). Một cỗ máy chiến tranh đáng gờm: Xây dựng và vận hành Bàn tay sắt của Archimedes [trực tuyến]. Truy cập ngày 10 tháng 6 năm 2017 tại cs.drexel.edu.
- VITE, L. (2014). Nguyên tắc của Archimedes [trực tuyến]. Truy cập ngày 10 tháng 6 năm 2017 tại repository.uaeh.edu.mx.


