Các tính năng của lăng kính hình trụ và cách tính khối lượng
Một lăng kính hình lăng trụ là một hình hình học, như tên gọi của nó, bao gồm hai định nghĩa hình học đó là: lăng kính và heptagon.
"Lăng kính" là một hình hình học được giới hạn bởi hai cơ sở là đa giác bằng nhau và song song và các mặt bên của chúng là hình bình hành.
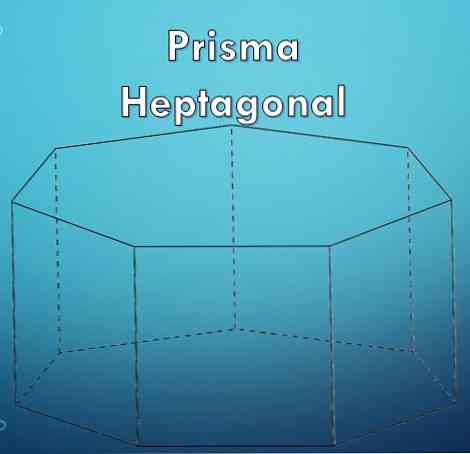
Một "heptagon" là một đa giác được hình thành bởi bảy (7) cạnh. Vì một hình khối là một đa giác, có thể là nó thường xuyên hoặc không đều.
Một đa giác được gọi là đều đặn nếu tất cả các cạnh của nó có cùng độ dài và góc bên trong của chúng giống nhau, chúng còn được gọi là đa giác đều; mặt khác người ta nói rằng đa giác không đều.

Đặc điểm của lăng kính hình lăng trụ
Sau đây là một số tính năng nhất định có lăng kính hình lăng trụ như: cấu trúc của nó, tính chất của các căn cứ của nó, diện tích của tất cả các mặt và thể tích của nó.
1- Xây dựng
Để xây dựng một lăng kính heptagonal cần có hai heptagons, đó sẽ là các cơ sở và bảy hình bình hành của nó, một ở mỗi bên của heptagon.
Bắt đầu bằng cách vẽ một hình khối, sau đó vẽ bảy đường thẳng đứng, có độ dài bằng nhau, xuất phát từ mỗi đỉnh của nó.
Cuối cùng, một heptagon khác được vẽ sao cho các đỉnh của nó trùng với điểm cuối của các đường được vẽ ở bước trước.
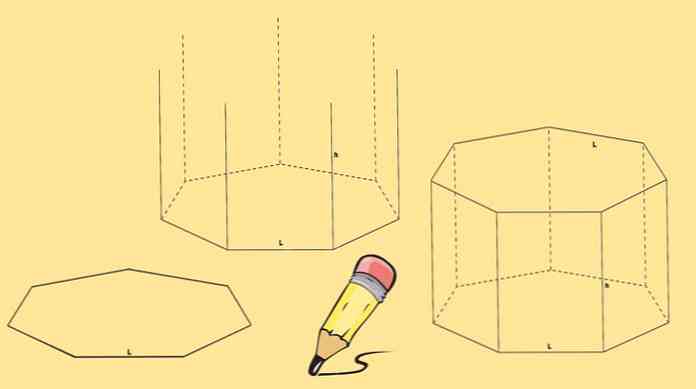
Lăng kính hình lăng trụ được vẽ ở trên được gọi là lăng kính hình lăng trụ thẳng. Nhưng bạn cũng có thể có một lăng kính hình lăng trụ xiên giống như trong hình dưới đây.

2- Tính chất của các cơ sở của nó
Vì các cơ sở của chúng là các heptagons, chúng tuân theo số đường chéo là D = nx (n-3) / 2, trong đó "n" là số cạnh của đa giác; trong trường hợp này ta có D = 7 × 4/2 = 14.
Chúng ta cũng có thể thấy rằng tổng các góc bên trong của bất kỳ heptagon (thông thường hoặc không đều) bằng 900º. Điều này có thể được xác minh bằng hình ảnh sau đây.
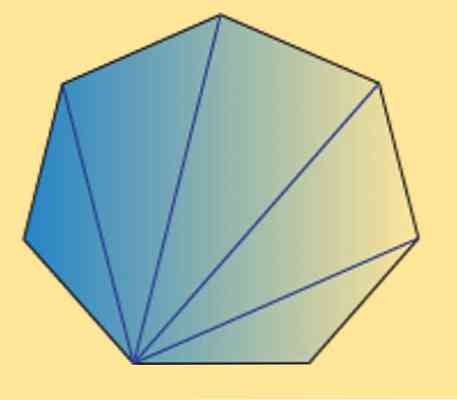
Như bạn có thể thấy, có 5 hình tam giác bên trong và sử dụng tổng các góc bên trong của một hình tam giác bằng 180º, có thể thu được kết quả mong muốn.
3- Diện tích cần thiết để xây dựng lăng kính hình lăng trụ
Vì các cơ sở của nó là hai heptagons và các cạnh của nó là bảy hình bình hành, nên diện tích cần thiết để xây dựng một lăng kính hình lăng trụ bằng 2xH + 7xP, trong đó "H" là diện tích của mỗi hình bình hành và "P" diện tích của mỗi hình bình hành.
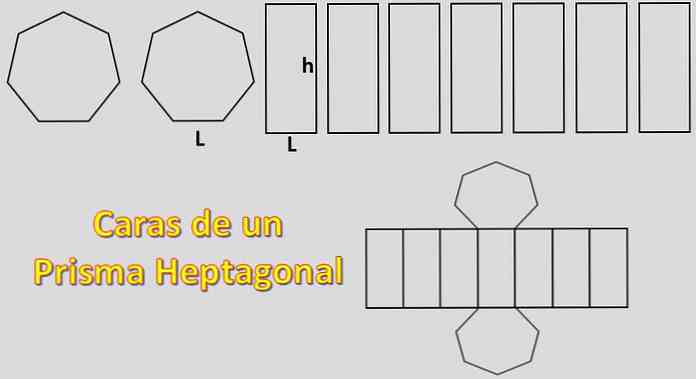
Trong trường hợp này, diện tích của một hình khối thông thường sẽ được tính toán. Đối với điều này, điều quan trọng là phải biết định nghĩa của apothema.
Apothem là một đường vuông góc đi từ tâm của một đa giác đều đến trung điểm của bất kỳ cạnh nào của nó.
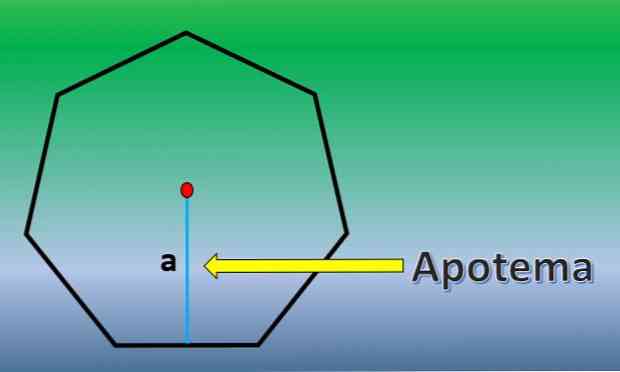
Khi đã biết apothem, diện tích của heptagon là H = 7xLxa / 2, trong đó "L" là chiều dài của mỗi bên và "a" chiều dài của apothem..
Diện tích của hình bình hành rất dễ tính toán, được định nghĩa là P = Lxh, trong đó "L" có cùng chiều dài của cạnh của hình khối và "h" là chiều cao của hình lăng trụ.
Tóm lại, lượng vật liệu cần thiết để xây dựng lăng kính hình lăng trụ (với các bazơ thông thường) là 7xLxa + 7xLxh, nghĩa là 7xL (a + h).
4- Khối lượng
Khi diện tích của một cơ sở và chiều cao của lăng kính đã biết, âm lượng được xác định là (diện tích cơ sở) x (chiều cao).
Trong trường hợp của một lăng kính hình lăng trụ (có cơ sở đều), nó có thể tích của nó là V = 7xLxaxh / 2; cũng có thể được viết là V = Pxaxh / 2, trong đó "P" là chu vi của hình vuông thông thường.
Tài liệu tham khảo
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Toán học: cách tiếp cận giải quyết vấn đề cho giáo viên giáo dục cơ bản. Biên tập viên López Mateos.
- Fregoso, R. S., & Carrera, S. A. (2005). Toán 3. Biên tập Progreso.
- Gallardo, G., & Pilar, P. M. (2005). Toán 6. Biên tập Progreso.
- Gutiérrez, C. T., & Cisneros, M. P. (2005). Khóa học toán 3. Biên tập Progreso.
- Kinsey, L., & Moore, T. E. (2006). Đối xứng, hình dạng và không gian: Giới thiệu về toán học thông qua hình học (minh họa, tái bản ed.). Khoa học & Truyền thông kinh doanh Springer.
- Mitchell, C. (1999). Thiết kế dòng Math rực rỡ (Minh họa chủ biên.). Scholastic Inc.
- R., M. P. (2005). Tôi vẽ 6º. Biên tập Progreso.


